Graph
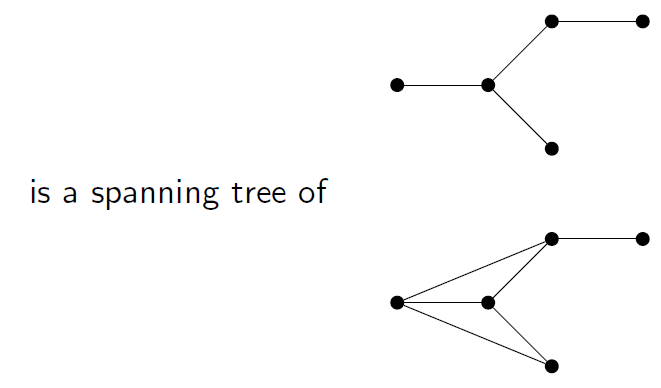
Multigraph : multiple edges or parallel edges除非强调,默认的图都是simple,就是说 不含loop和parallel edges Directed graphs 有向图 Walk 一系列点,每一个都连着下一个 A walk is a sequence of vertices where each vertex is adjacent to the next. A path is a walk consisting of distinct vertices. 路径是由不同的顶点组成的遍历 If every pair of vertices have a path (or a walk) between them, then we say the graph is connected. 每一个顶点都有路径 The degree of a vertex is the number of edges that include that vertex. (Degree是顶点边的数量) If every vertex has the same degree k, then we say the graph is k-regular. Connected性质:sum of the degrees equals twice the number of edges. the sum of the degrees is even偶数 A tree is a connected graph with no cycles. A tree with n vertices has n-1 edges. spanning tree 生成树 Every connected graph G contains a spanning tree. 由图生成一棵树,包括图的所有顶点,只留一条边,去掉所有循环
If two vertices are joined by an edge they are adjacent. 相邻接的 adjacency matrix 见上图 Number of walks计算??
Euler circuit 回到原点,闭合walk,每边就用一次 A connected graph is Eulerian if and only if every vertex has an even degree. Euler trail 不用回到原点,闭合walk,每边就用一次 A connected graph has an Euler trail if and only if at most two vertices have odd degrees. 最多两个顶点是奇数 Hamilton cycle: visits each vertex exactly once.

